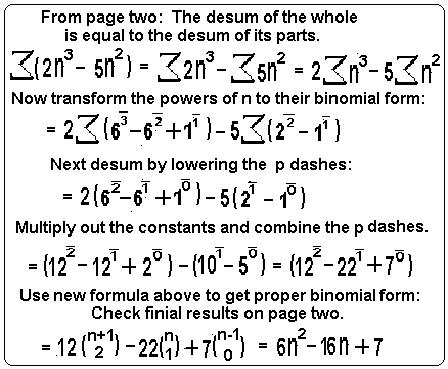
Same Web page, as published around 1996, formerly bbcorn as my dad was known. - Top lineWritten by Robert Koernke Jr.
Desummation
by Robert E. Koernke SR
Purpose of the Desummation Article
Desummation Discussion:
"Given a polynomial of one variable to whatever degree, is it possible to find the polynomial that when summed equals the polynomial given?" To get the results I wanted I used the following logic:


From Desummation To Binomial Transformation
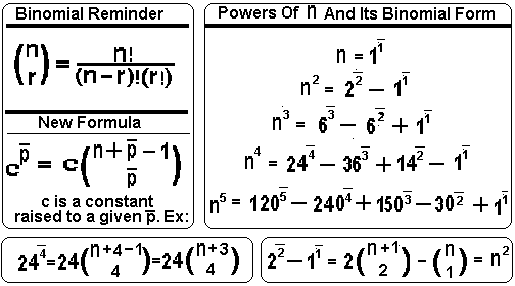
What if, after desumming the first time, the desummathion process continues for any powers of n that remain? Note that a constant can't be desumed. When a constant appears after a desum then simply label it by the number of desums it took to appear. Labels can look like exponents but with a dash above it.
Take n squared for an example of a complete desummation The first desum of n squared is (2n-1). Note that (-1) appears at the first desum so label it with a one like any exponent with a dash above it. Now (2n) is left and the desum of 2n = 2. Since the 2 appeared at the second desum it is labeled with a 2 dash. So the complete desum of n squared is '2 to the 2 dash minus 1 to the 1 dash'.
Here is a list of the complete desums of the first five powers of n:
![]()
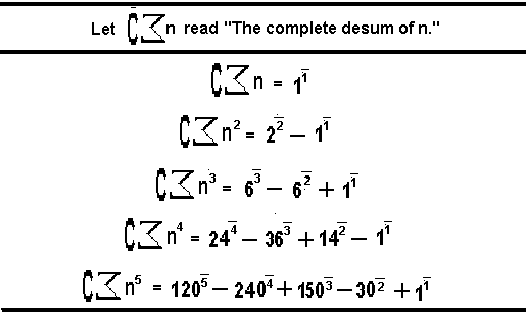
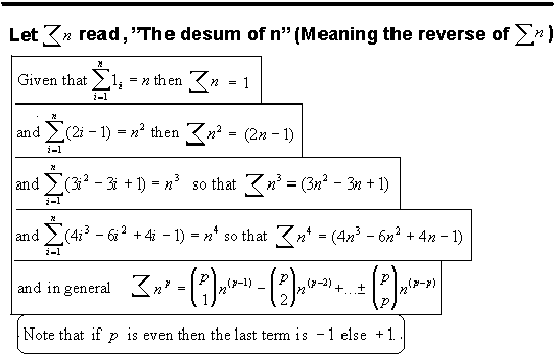
Note that the first term in each row is a factorial. The last term is plus one if the row is odd else minus one if the row is even. (A good way to check a row is to add it. Each row adds up to one.) The inside terms are found by the following formula:
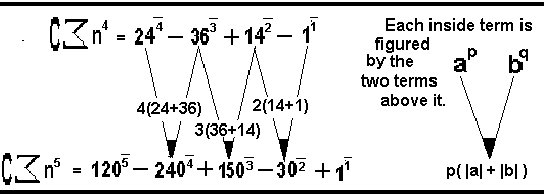
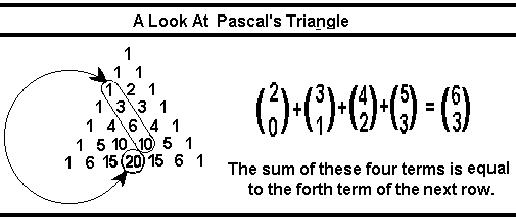
The idea that I was looking at values in Pascal's Triangle became very interesting. I recalled that the sum of n terms in any diagonal row in Pascal's Triangle is found to be the nth term of the next row down.
I tried the formula on these values and it worked. What I now have is a method of changing powers of n into its binomial form. In this form to sum simply add one to the p dash or subtract one to desum... I will give two formulas and some examples: